trilateration.md (7987B)
Trilatération
La trilatération permet de déduire la position d'un point grâce à sa distance avec 3 autres points dont on connaît déjà la position. Dans le système GPS les satellites envoient régulièrement :
- leur coordonnées précises ;
- l'heure à laquelle ils envoient les données.
En recevant ces messages de 3 satellites ou plus, et en connaissant l'heure précise de réception des messages, on peut retrouver notre position.
Voyons d'abord comment mesurer la distance qui nous sépare d'un satellite.
Distance
Quand on reçoit un message d'un satellite on connaît :
- l'heure précise d'envoi du message, puisque le satellite la met dans le message et qu'il embarque une horloge atomique ;
- l'heure précise d'arrivée du message, à condition d'avoir une horloge bien à l'heure.
La différence entre ces 2 heures est le temps que le message à mis à parcourir l'espace entre l'émétteur (le satellite) et le récepteur GPS.
Par exemple si un message est :
- envoyé à *19 heures 23 minutes 05 secondes et 230 millisecondes*
- reçu à *19 heures 23 minutes 05 secondes et 683 millisecondes*
Il aura mis 683 - 230 = 453 ms à arriver.
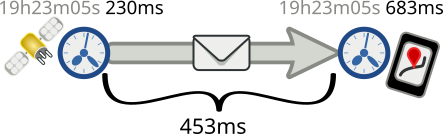
Comme le message est envoyé par onde radio, il se déplace à la vitesse de la lumière, donc à peu près 300km/ms.
Dans notre exemple, on est donc à $453\times300=135900$ km du satellite.
Question :
Si on reçoit le message d'un satellite :
- envoyé à *13 heures 37 minutes 42 secondes et 100 millisecondes*
- reçu à *13 heures 37 minutes 42 secondes et 200 millisecondes*
Donnez la distance (en km) qui nous sépare du satellite :
(en considérant toujours que le message se déplace à 300km/ms)
km
Trilatération
Si on connaît notre distance à un seul satellite, et les coordonnées de ce satellite, on ne peut pas connaître notre position exacte, mais on sait qu'on est sur le cercle qui a pour centre le satellite et pour rayon cette distance.
Par exemple ici on pourraît être n'importe où sur le cercle orange :
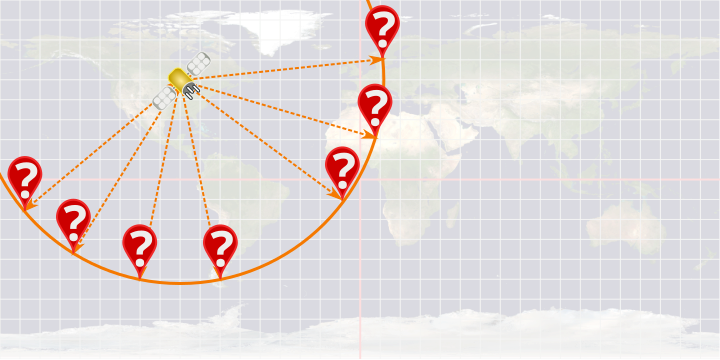
Si on connait la position et la distance à 2 satellites, il ne reste que 2 possibilités : les 2 points où les cercles se croisent.
Exemple :
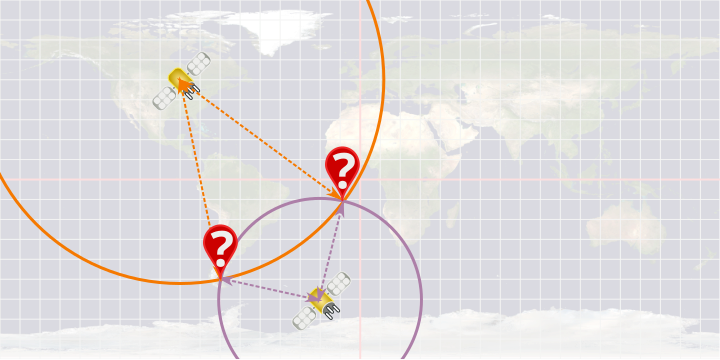
Donc pour connaître notre position exacte on a besoin de 3 satellites. Les 3 cercles qui ont pour centre les satellites et pour rayon la distance entre le satellite et le récepteur se croisent en un point aui est à la position exacte du récepteur. Cette méthode s'appelle la trilatération.
Exemple :
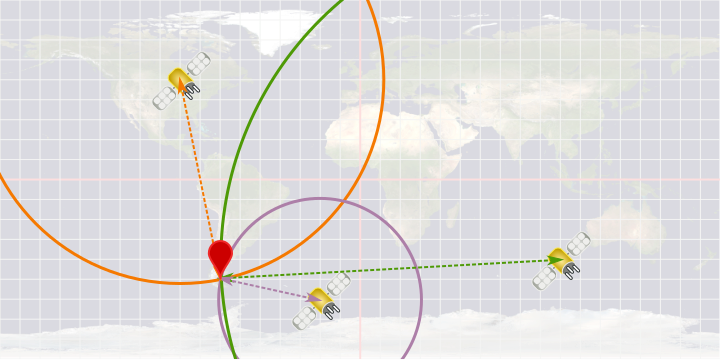
En réalité dans le système GPS il y a toujours au minimum 4 satellites dont on reçoit les message à tout moment : ça permet d'être plus précis, notamment si on n'est pas sûr que l'horloge d'un appareil est suffisement précise.
Question :
On veut trouver notre position grâce au système GPS. On capte les messages des 3 satellites A, B, et C.
En comparant l'heure d'arrivée et de départ des messages reçus on en déduit que :
- A est à 216 ms de nous,
- B est à 201 ms de nous,
- C est à 223 ms de nous.
Grâce aux coordonnées contenues dans les messages des satellites, on a pu les replacer sur une carte :
Vous pouvez régler l'affichage des distances des satellites grâce aux glissières suivantes :
Distance au satellite A : [40]{#satdstlabel0} ms.
Distance au satellite B : [40]{#satdstlabel1} ms.
Distance au satellite C : [40]{#satdstlabel2} ms.
Trouvez la position de notre récepteur GPS par trilatération.
Déduisez-en les coordonnées géographiques de notre récepteur :
(Rappel : les lignes horizontales et verticales sont placées tous les 10°)
° , °